Tổng quan
Đây là câu hỏi không biết bao nhiêu người đã hỏi mình trong suốt những năm qua và khiến mình cảm thấy khó chịu đến mức chúng lặp lại hàng trăm lần đối với tất cả các kỹ sư mới bước chân vào tìm hiểu Dynamo hoặc công việc tự động hóa, xử lý hình học,... Vậy thì hôm nay chúng ta cùng làm rõ ràng việc các kỹ sư muốn kiểm tra nhanh một điểm có nằm trong phòng không nhé.
Việc này được ứng dụng rộng rãi trong những việc sau :
- Kiểm tra nhanh một điểm trong khu vực phòng.
- Kiểm tra xung đột
- Kiểm tra nhanh các thiết bị có nằm trong phòng hay không
- Thống kê số lượng các thiết bị trong phòng
- ...
Để tiếp nối bài viết Convert Point Cloud From LiDAR Mobile To Speckle ở kì trước. Chúng ta sẽ dễ dàng ví dụ tiếp theo cho bài viết này. Mục tiêu của bài hướng dẫn này là tiếp tục làm rõ các xác định xem chiếc ghế của mình đang được đặt bên ngoài phòng hay bên trong phòng.
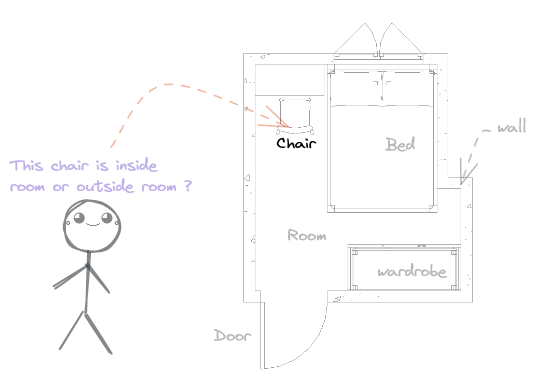
Đây là căn phòng mà chúng ta sẽ tiếp tục trong bài viết này.
Tìm Room và kiểm tra điểm có nằm trong phòng hay không
Việc tìm room là khá đơn giản, với việc lựa chọn room cho phép bạn xác định ngay từ đầu các room muốn kiểm tra nhanh và việc chọn ghế cũng tương tự như vậy..
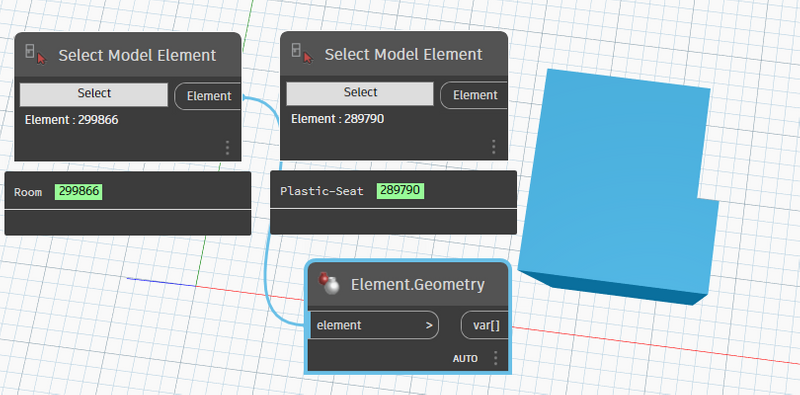
Và việc kiểm tra xem một family có tồn tại bên trong một room hay không chỉ đơn giản là sử dụng Node FamilyInsntace.Location và Room.IsInsideRoom như sau :
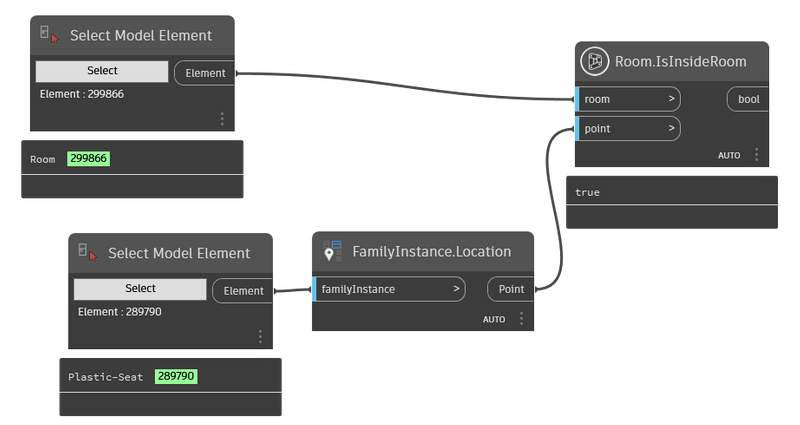
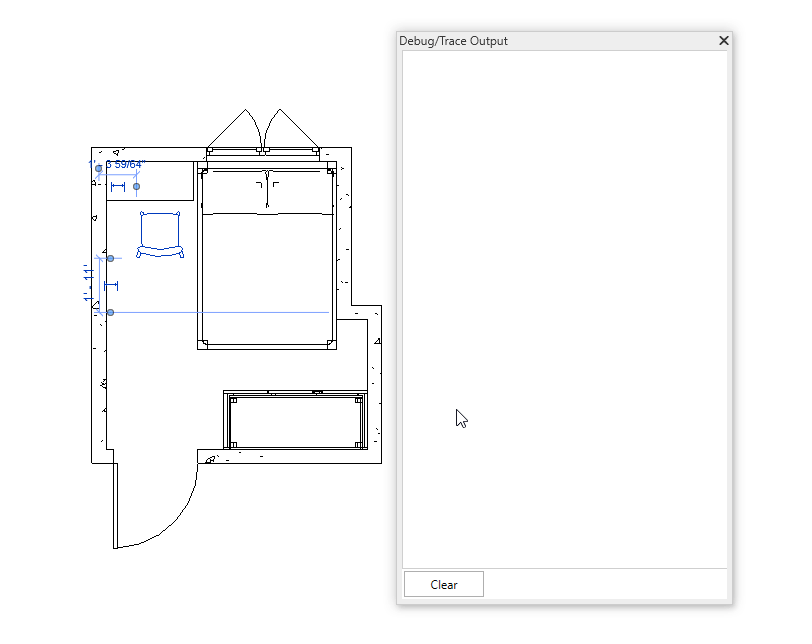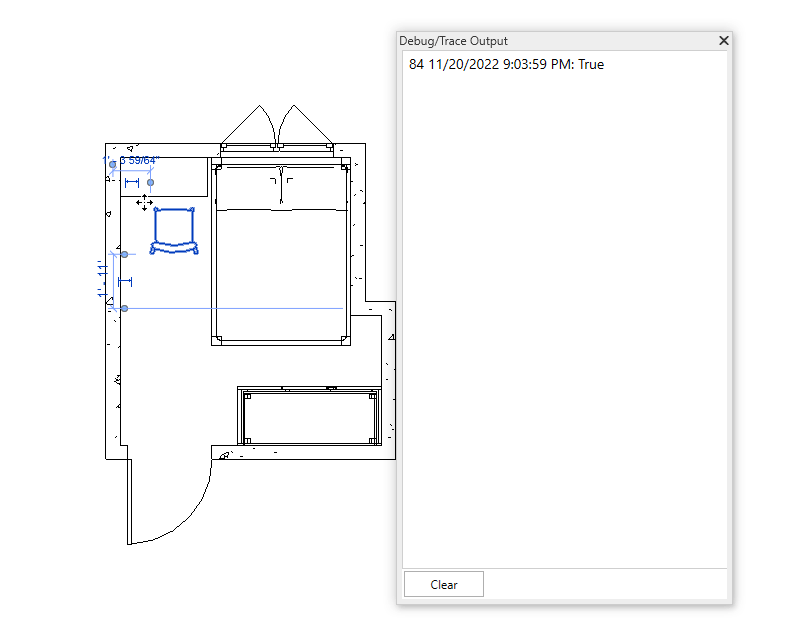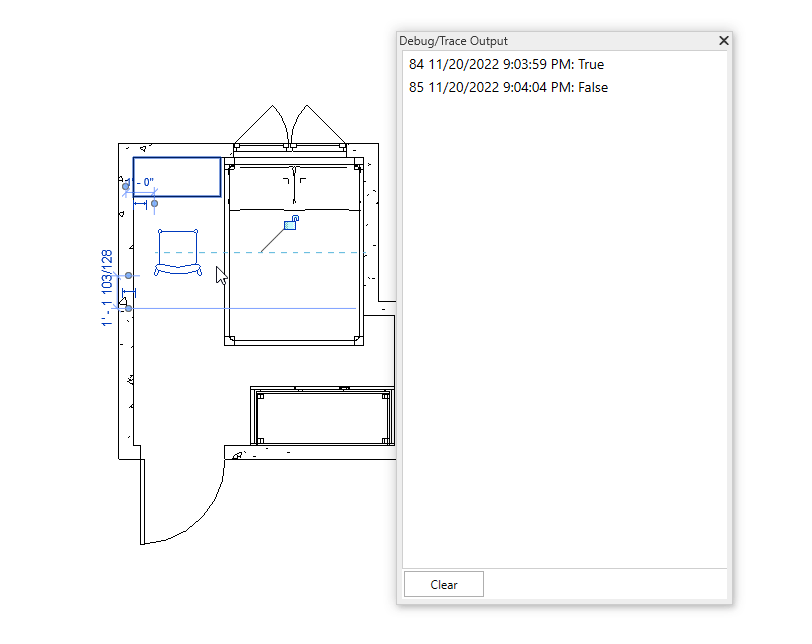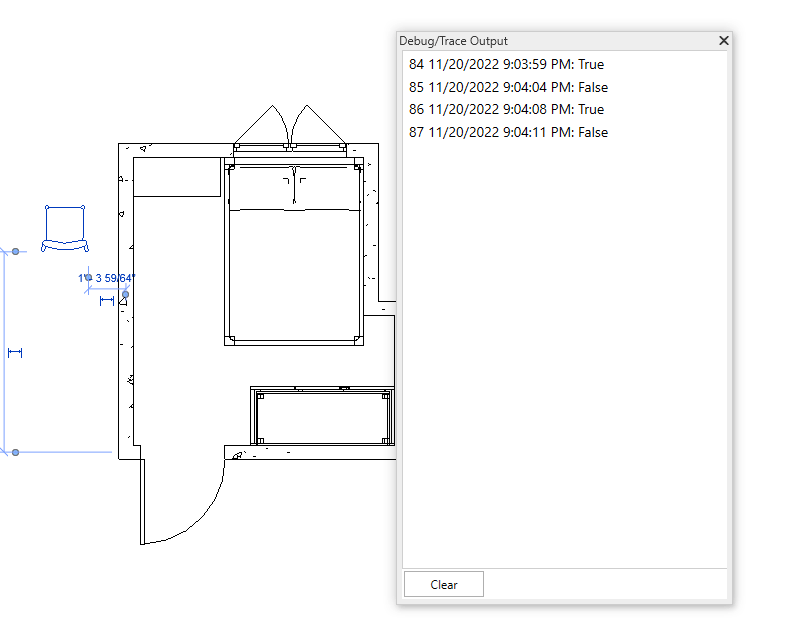
Bây giờ chúng ta sẻ thử di chuyển chiếc ghế ra khỏi phòng và di chuyển trở lại căn phòng để kiểm tra tính thực tế của chúng.
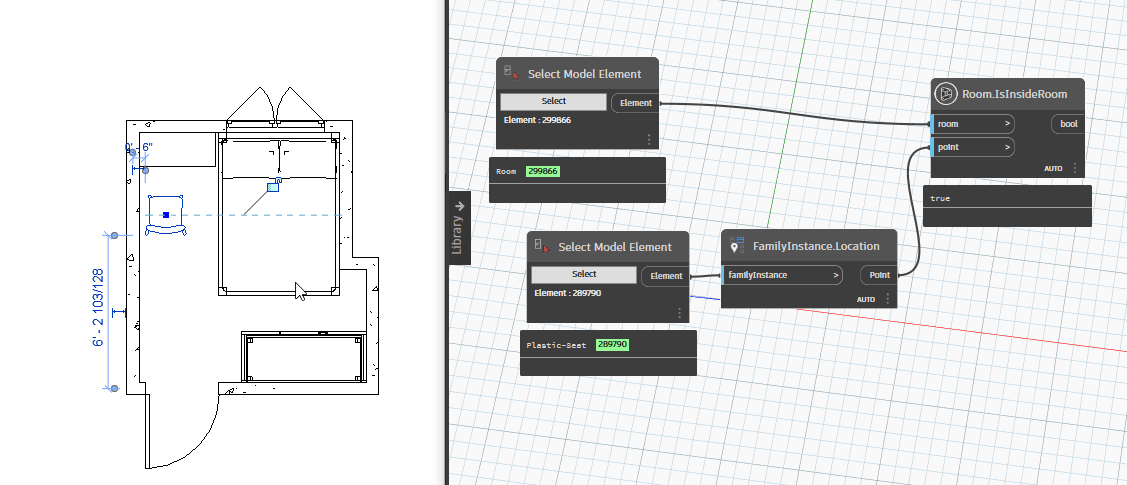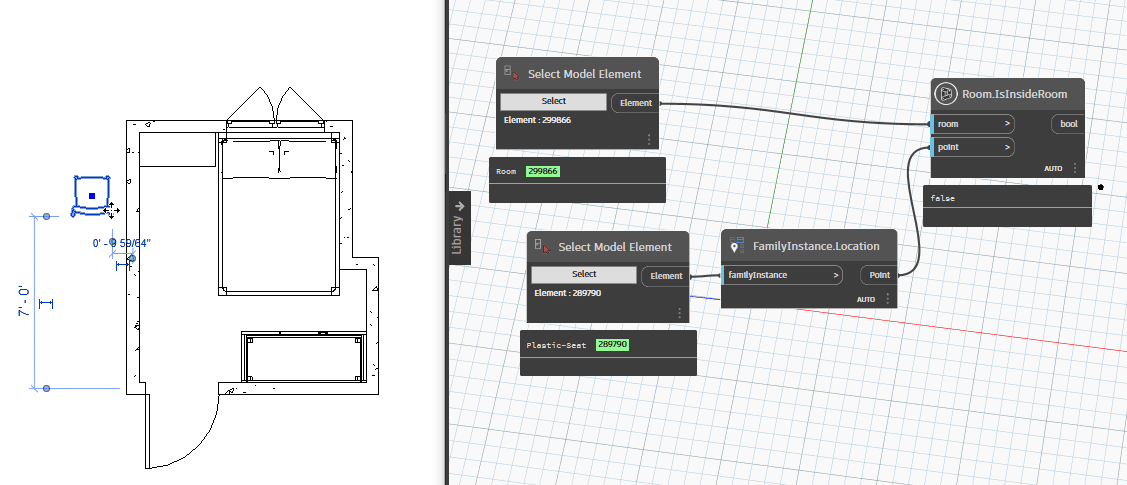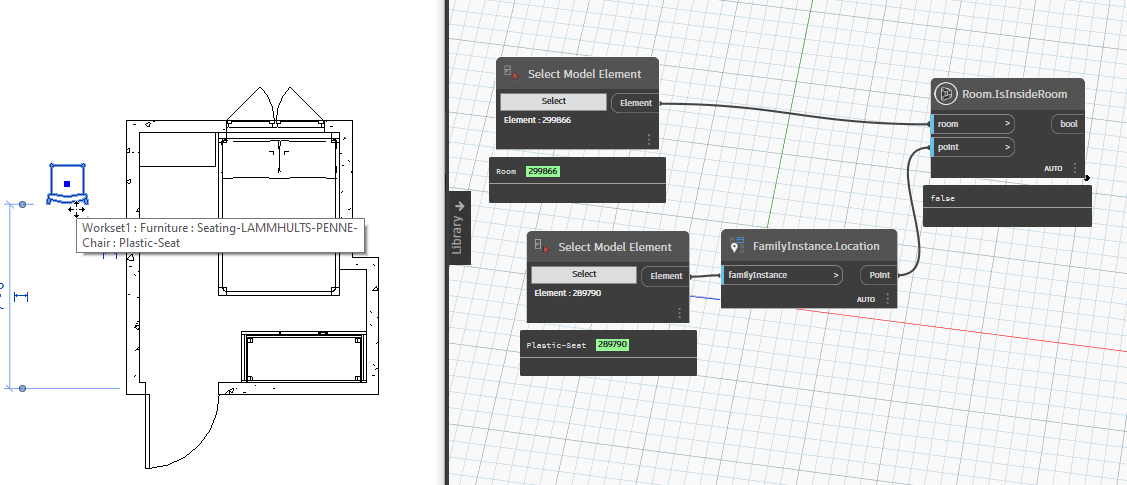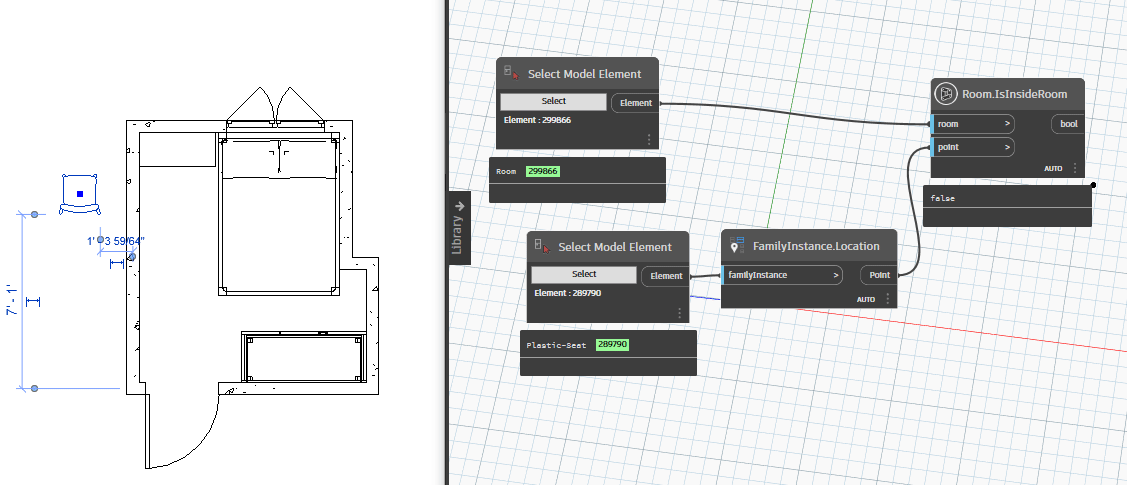
Như vậy với kết quả kiểm tra, giá trị đã nhanh chóng thay đổi từ true sang false và ngược lại. Điều này cho thấy rằng chúng ta đã có thể kiểm tra nhanh một family có nằm trong phòng hay không. Điều này cũng đồng nghĩa với việc kiểm tra nhanh một điểm có nằm trong phòng hay không.
Lưu ý : Các lớp tường là rất quan trọng nên chú ý trước khi kiểm tra, đồng thời việc loại bỏ các room có tiết diện bằng 0 giúp bạn tránh khỏi các phòng lỗi và việc ngừng sử dụng các hàm liên quan đến trực quan hóa đối tượng hình học giúp bạn tránh được các vấn đề về hiệu suất với Dynamo.
Tự tạo lại hàm kiểm tra với Revit API
Rất nhiều người đã tò mò và muốn đi đến cùng để xem liệu làm thế nào mà Node Room.IsInsideRoom đã có thẻ kiểm tra nhanh như vậy. Vậy thì chúng ta cũng cùng đi đến gốc rễ của vấn đề này luôn, luôn có những anh chàng tò mò chả bao giờ chịu dừng lại ở sự đơn giản, đặc biệt là các kỹ sư tinh nghịch.

Có rất nhiều cách để bạn có thể tự làm cho riêng mình, nhưng đây là một số cách phổ biến :
- Sử dụng Revit API từ method IsPointInRoom
- Tạo lại cho mình thuật toán không phụ thuộc vào Revit API.
Để đơn giản hơn, bạn có thể xem qua mã đơn giản bên dưới để giúp kiểm tra nhanh một điểm có nằm trong phòng hay không thông qua Revit API với cách (1).
| var Id1 = 299866; | |
| var Id = 289790; | |
| var roomid = new Autodesk.Revit.DB.ElementId(Id1); | |
| var chairId = new Autodesk.Revit.DB.ElementId(Id); | |
| Room room = (Room)Doc.GetElement(roomid); | |
| var chair = (FamilyInstance)Doc.GetElement(chairId); | |
| LocationPoint locationPoint = (LocationPoint) chair.Location; | |
| XYZ chairlc = locationPoint.Point; | |
| bool isPointInRoom = room.IsPointInRoom(chairlc); | |
| Trace.WriteLine(isPointInRoom); | |
| return; |
Sử dụng công cụ RevitAddInManager với tính năng trace output để xem kết quả nhanh từ bảng panel như mẫu bên dưới.
Được rồi, chúng ta hãy sang vấn đề với cách 2 để thỏa mãn thứ mà chúng ta muốn hướng đến.
Xây dựng thuật toán kiểm tra (2).
Ở phần này giúp giải quyết vấn đề với những anh chàng đã đến đỉnh cao và muốn khám phá tường tận đến cuối cùng. Vậy thì chúng ta hãy cùng xem liệu thật sự làm thế nào để kiểm tra một điểm có nằm trong phòng hay không. Làm thế nào mà chúng ta có thể tự tạo ra mà không dựa vào các API có sẵn ? Có rất nhiều anh chàng hỏi mình là đã có API vậy sao chúng ta cần phải xây dựng lại. Vậy thì bạn nên hỏi rằng, nếu một ngày nọ bạn cần tùy chỉnh vấn đề đến mức cao nhất, ai sẽ là người tạo ra các API đó giúp bạn hay hỗ trợ bạn, hay chính bạn phải làm ra nó ?

Điểm bên trái hay bên phải cạnh
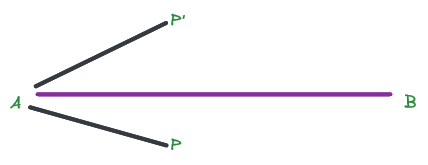
Bây giờ mình đang có một đoạn thẳng AB và Điểm P và P' nằm bên trái và bên phải, vậy bây giờ làm thế nào để xác định xem là P,P' đang nằm bên trái hay bên phải. Thực tế vấn đề này chúng ta hãy quy đổi sang toán học một chút, đó là xác định xem hai điểm đang ở cùng hướng hay khác hướng. Hướng ở đây chính là bên trái và bên phải. Như vậy chúng ta sẽ tránh được một số tranh cãi không đáng có.
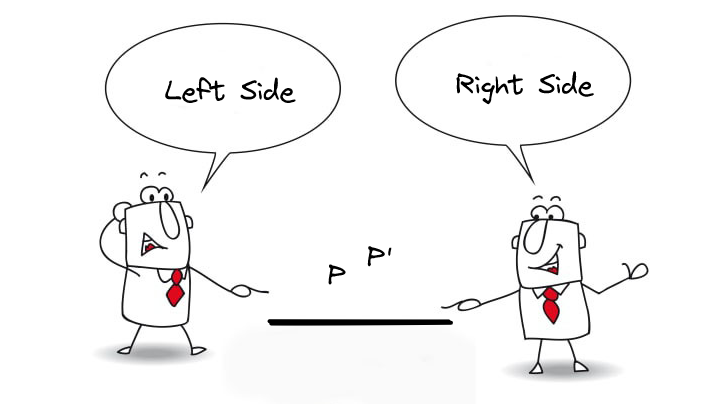
Nếu bạn lấy tích có hướng (CrossProduct) của [BA] và [pA], bạn sẽ nhận được một vectơ chỉ ra khỏi màn hình. Mặt khác, nếu bạn lấy tích có hướng (Cross Product) của [BA] và [p'-A] bạn sẽ có một véc-tơ hướng vào màn hình. Trong thực tế nếu bạn sử dụng phép vô hướng [BA] với vectơ từ A đến bất kỳ điểm nào trên đường thẳng AB, vectơ kết quả chỉ ra bên ngoài trong khi sử dụng bất kỳ điểm bên dưới AB tạo ra một vectơ trỏ vào bên trong. Vì vậy tất cả những gì chúng ta cần làm để phân biệt một điểm nằm trên cạnh nào của một đường thẳng là lấy một tích chéo (Cross Product). Và nếu tích vô hướng(Dot Product) của hai vectơ là dương thì hai vectơ cùng hướng, nếu là âm thì hai vectơ khác hướng. Điều này đã được mình giải thích rõ ràng trong bài Dot Product And Cross Product In Dynamo.
Như vậy ta có thể nhanh chóng viết một mã kiểm định nhanh hướng với p1,p2 là hai điểm cần kiểm tra và a,b là hai điểm đoạn thẳng AB. :
| bool IsSamSide(XYZ p1, XYZ p2, XYZ a, XYZ b) | |
| { | |
| XYZ cp1 = (p1 - a).CrossProduct(b - a); | |
| XYZ cp2 = (p2 - a).CrossProduct(b - a); | |
| return cp1.DotProduct(cp2) >= 0; | |
| } |
Việc và với việc sử dụng DirectShape sẽ trực quan hóa giúp bạn có cái nhìn cụ thể về việc kiểm định hướng của hai điểm. Nếu màn hình hiển thị kết quả True đồng nghĩa với cùng hướng và False đồng nghĩa với khác hướng.
| using Autodesk.Revit.Attributes; | |
| using Autodesk.Revit.DB; | |
| using Autodesk.Revit.UI.Selection; | |
| using Line = Autodesk.Revit.DB.Line; | |
| using Point = Autodesk.Revit.DB.Point; | |
| var Doc = commandData.Application.ActiveUIDocument.Document; | |
| using TransactionGroup trang = new TransactionGroup(Doc, "test"); | |
| trang.Start(); | |
| XYZ a = UIDoc.Selection.PickPoint(ObjectSnapTypes.None); | |
| SetPoint(a); | |
| XYZ b = UIDoc.Selection.PickPoint(ObjectSnapTypes.None); | |
| SetPoint(b); | |
| SetLine(a,b); | |
| XYZ p1 = UIDoc.Selection.PickPoint(ObjectSnapTypes.None); | |
| SetPoint(p1); | |
| XYZ p2 = UIDoc.Selection.PickPoint(ObjectSnapTypes.None); | |
| SetPoint(p2); | |
| bool isSamSide = IsSamSide(p1, p2, a, b); | |
| MessageBox.Show(isSamSide.ToString()); | |
| trang.Assimilate(); | |
| // visualize a point | |
| void SetPoint(XYZ xyz) | |
| { | |
| using (Transaction tran = new Transaction(Doc, "Add point")) | |
| { | |
| tran.Start(); | |
| Point point1 = Point.Create(xyz); | |
| DirectShape ds = | |
| DirectShape.CreateElement(Doc, new ElementId(BuiltInCategory.OST_GenericModel)); | |
| ds.SetShape(new List<GeometryObject>() {point1}); | |
| tran.Commit(); | |
| } | |
| } | |
| // visualize a line | |
| void SetLine(XYZ x1,XYZ x2) | |
| { | |
| using (Transaction tran = new Transaction(Doc, "Add line")) | |
| { | |
| tran.Start(); | |
| Line line = Line.CreateBound(x1, x2); | |
| DirectShape ds = | |
| DirectShape.CreateElement(Doc, new ElementId(BuiltInCategory.OST_GenericModel)); | |
| ds.SetShape(new List<GeometryObject>() {line}); | |
| tran.Commit(); | |
| } | |
| } |

Tìm điểm bên trong tam giác
Một cách phổ biến để kiểm tra xem một điểm có nằm trong tam giác hay không là tìm các vectơ nối điểm với ba đỉnh của tam giác và tính tổng góc giữa các vectơ đó. Nếu tổng các góc là 2*pi thì điểm nằm bên trong tam giác, ngược lại thì không. Nó hoạt động, nhưng nó rất chậm. Dưới đây sẽ giải thích một phương pháp nhanh hơn và dễ dàng hơn nhiều.

Được rồi, ABC tạo thành một hình tam giác và tất cả các điểm bên trong nó chính là vùng màu trắng như hình. Các đường thẳng AB, BC và CA mỗi không gian cắt nhau và tạo ra các phần màu khác nằm hoàn toàn bên ngoài hình tam giác. Để một điểm nằm bên trong tam giác ABC thì nó phải nằm dưới AB và bên trái BC và bên phải của AC. Đó là những gì chúng ta sẽ tận dụng từ việc xác định hướng của hai điểm đã giải quyết ở phần trên.
Như vậy có thể tóm gọn lại, khi bạn thả một điểm P vào vùng màu trắng, Nếu kiểm tra hướng của ba đoạn thẳng AB,BC,CA đồng thời thỏa mãn P cùng hướng thì chắn chắn rằng điểm P đó nằm trong tam giác. Kết hợp với các hàm trên ta có thể viết được hàm kiểm tra điểm có nằm trong tam giác hay không.
| bool PointInTriangle(XYZ p, XYZ a, XYZ b, XYZ c) | |
| { | |
| if(IsSamSide(p,a,b,c) && IsSamSide(p,b,a,c) && IsSamSide(p,c,a,b)) | |
| return true; | |
| return false; | |
| } |
Giành một chút thời gian để kiểm nghiệm lại tính đúng đắn tương tự như với đoạn thẳng. Ở đây chúng ta sẽ chấm ba điểm, nối ba điểm tạo ra một tam giác và chọn một điểm để kiểm tra kết quả, nếu kết quả trả về True tức là bên trong tam giác, ngược lại thì không.
| using TransactionGroup trang = new TransactionGroup(Doc, "test"); | |
| trang.Start(); | |
| XYZ a = UIDoc.Selection.PickPoint(ObjectSnapTypes.None); | |
| SetPoint(a); | |
| XYZ b = UIDoc.Selection.PickPoint(ObjectSnapTypes.None); | |
| SetPoint(b); | |
| SetLine(a,b); | |
| XYZ c = UIDoc.Selection.PickPoint(ObjectSnapTypes.None); | |
| SetPoint(c); | |
| SetLine(b,c); | |
| SetLine(a,c); | |
| XYZ p = UIDoc.Selection.PickPoint(ObjectSnapTypes.None); | |
| SetPoint(p); | |
| bool pointInTriangle = PointInTriangle(p, a, b, c); | |
| MessageBox.Show(pointInTriangle.ToString()); | |
| trang.Assimilate(); | |
| // visualize a point | |
| void SetPoint(XYZ xyz) | |
| { | |
| using (Transaction tran = new Transaction(Doc, "Add point")) | |
| { | |
| tran.Start(); | |
| Point point1 = Point.Create(xyz); | |
| DirectShape ds = | |
| DirectShape.CreateElement(Doc, new ElementId(BuiltInCategory.OST_GenericModel)); | |
| ds.SetShape(new List<GeometryObject>() {point1}); | |
| tran.Commit(); | |
| } | |
| } | |
| // visualize a line | |
| void SetLine(XYZ x1,XYZ x2) | |
| { | |
| using (Transaction tran = new Transaction(Doc, "Add line")) | |
| { | |
| tran.Start(); | |
| Line line = Line.CreateBound(x1, x2); | |
| DirectShape ds = | |
| DirectShape.CreateElement(Doc, new ElementId(BuiltInCategory.OST_GenericModel)); | |
| ds.SetShape(new List<GeometryObject>() {line}); | |
| tran.Commit(); | |
| } | |
| } |

Tìm điểm bên trong đa giác.
Mở rộng vấn đề lên một chút và quay lại với căn phòng của chúng ta. Rất tiếc căn phòng của chúng ta không phải là hình tam giác. Kiểm định tam giác chỉ là bước khởi đầu cho sự hiểu biết đơn giản tiếp cận vấn đề mà thôi. Vấn đề bây giờ mới thật sự đang diễn ra, chúng ta hãy bắt đầu tìm điểm bên trong một đa giác bất kì, cũng như Room, số lượng đường bao của Room chính là số điểm của đa giác đó, và Family chính là điểm trực thuộc bên trong điểm của một đa giác hay bên ngoài của một đa giác.
Một thuật toán đơn giản nhất có thể xử lý điều này là thuật toán truyền tia. Ý tưởng của thuật toán khá đơn giản: Vẽ một tia ảo từ bất kỳ đâu bên ngoài đa giác đến điểm của bạn và đếm tần suất tia đó chạm vào một cạnh của đa giác. Nếu số lần bắn là chẵn thì nằm ngoài đa giác, nếu lẻ thì nằm trong đa giác.
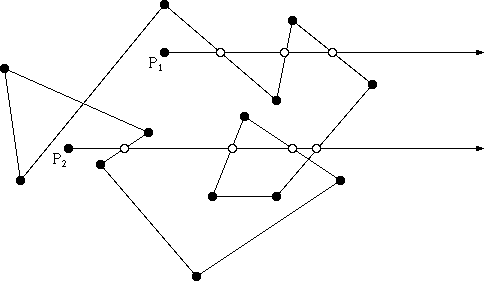
Hay thuật toán Winding number của Dan Sunday. Số quanh co bằng 0 có nghĩa là điểm nằm ngoài đa giác, các giá trị khác cho biết điểm nằm trong đa giác
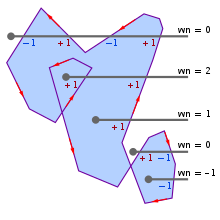
Truyền tia sang phải được xem là thuật toán đẹp với ít dòng mã nhất. Mỗi lần lặp lại của vòng lặp, điểm kiểm tra được kiểm tra đối với một trong các cạnh của đa giác. Dòng đầu tiên của kiểm tra nếu thành công nếu tọa độ y của điểm nằm trong phạm vi của cạnh. Dòng thứ hai kiểm tra xem điểm kiểm tra có ở bên trái của Line hay không.
Bằng cách liên tục đảo ngược giá trị của coordinates, thuật toán sẽ đếm số lần đường thẳng đi qua đa giác. Nếu nó đi qua một số lẻ lần, thì điểm nằm bên trong; nếu là số chẵn thì điểm nằm ngoài.
Chúng ta có thể viết một hàm để kiểm tra nhanh như sau, với RoomPoint đã được định nghĩa lại và PolyLine bạn cũng có thể làm điều tương tự cho việc khởi tạo lại các đỉnh và công thức nối đỉnh.
| // check point in polyline | |
| bool IsPointInPolygon(PolyLine poly, RoomPoint testPoint) | |
| { | |
| bool result = false; | |
| IList<XYZ> coordinates = poly.GetCoordinates(); | |
| int j = coordinates.Count() - 1; | |
| for (int i = 0; i < coordinates.Count(); i++) | |
| { | |
| if (coordinates[i].Y < testPoint.Y && coordinates[j].Y >= testPoint.Y || | |
| coordinates[j].Y < testPoint.Y && coordinates[i].Y >= testPoint.Y) | |
| { | |
| if (coordinates[i].X + (testPoint.Y - coordinates[i].Y) / (coordinates[j].Y - coordinates[i].Y) * | |
| (coordinates[j].X - coordinates[i].X) < testPoint.X) | |
| { | |
| result = !result; | |
| } | |
| } | |
| j = i; | |
| } | |
| return result; | |
| } | |
| // define again a point. | |
| public class RoomPoint | |
| { | |
| public double X { get; set; } | |
| public double Y { get; set; } | |
| public double Z { get; set; } | |
| public RoomPoint(double x, double y, double z) | |
| { | |
| this.X = x; | |
| this.Y = y; | |
| this.Z = Z; | |
| } | |
| } |
Một hàm để hiển thị kết quả trực quan giúp bạn trên Revit API. Ở đây chúng ta sẽ pick chọn bao nhiêu điểm để tạo ra một đa giác bất kỳ, sau đó chọn một điểm để kiểm tra nó có nằm trong đa giác hay không. DirectShape cho phép vẽ ra các hình học trực quan hóa như ví dụ đầu tiên đã trình bày. Danh sách điểm trong PolyLine sẽ được thêm vào điểm đầu với mục đích nối đoạn thẳng thành đa giác kết thúc chu kỳ vòng bao của một đa giác thông qua các đỉnh.
| using System.Text; | |
| using System.Windows; | |
| using Autodesk.Revit.Attributes; | |
| using Autodesk.Revit.DB; | |
| using Autodesk.Revit.UI.Selection; | |
| using Line = Autodesk.Revit.DB.Line; | |
| using Point = Autodesk.Revit.DB.Point; | |
| var Doc = commandData.Application.ActiveUIDocument.Document; | |
| using (TransactionGroup transactionGroup = new TransactionGroup(Doc, "add")) | |
| { | |
| transactionGroup.Start(); | |
| List<XYZ> points = new List<XYZ>(); | |
| int i = 0; | |
| StringBuilder sb = new StringBuilder(); | |
| while (true) | |
| { | |
| try | |
| { | |
| XYZ point = UIDoc.Selection.PickPoint(ObjectSnapTypes.None); | |
| using (Transaction tran = new Transaction(Doc, "Add point")) | |
| { | |
| tran.Start(); | |
| Point point1 = Point.Create(point); | |
| sb.AppendLine(point1.ToString()); | |
| DirectShape ds = | |
| DirectShape.CreateElement(Doc, new ElementId(BuiltInCategory.OST_GenericModel)); | |
| ds.SetShape(new List<GeometryObject>() {point1}); | |
| points.Add(point); | |
| tran.Commit(); | |
| } | |
| } | |
| catch (Exception) | |
| { | |
| break; | |
| } | |
| } | |
| if(points.Count<3) throw new ArgumentException("Need at least 3 points"); | |
| using Autodesk.Revit.DB.Transaction trans = new Transaction(Doc,"Add PolyLine"); | |
| trans.Start(); | |
| if(points[0].DistanceTo(points[points.Count-1])>0.001) | |
| points.Add(points[0]); | |
| PolyLine polyLine = Autodesk.Revit.DB.PolyLine.Create(points); | |
| DirectShape dspoly = | |
| DirectShape.CreateElement(Doc, new ElementId(BuiltInCategory.OST_GenericModel)); | |
| dspoly.SetShape(new List<GeometryObject>() {polyLine}); | |
| trans.Commit(); | |
| trans.Start(); | |
| XYZ checkPoint = UIDoc.Selection.PickPoint(ObjectSnapTypes.None,"Pick Point To Check"); | |
| RoomPoint roomPoint = new RoomPoint(checkPoint.X, checkPoint.Y, 0); | |
| bool flag = IsPointInPolygon(polyLine, roomPoint); | |
| dspoly.AppendShape(new List<GeometryObject>(){Point.Create(checkPoint)}); | |
| trans.Commit(); | |
| MessageBox.Show(flag.ToString()); | |
| transactionGroup.Assimilate(); | |
| } |
Kiểm nghiệm tính chính xác của thuật toán. Nếu kết quả trả về là true thì nằm trong đa giác, ngược lại nằm ngoài đa giác.

Kiểm tra vị trí ghế với Speckle
Đây là lúc chúng ta cần tùy chỉnh lại một chút để phù hợp với mô hình Speckle. Ở đây mình sẽ ví dụ cho bạn kiểm tra xem liệu chiếc ghế này có thuộc sàn không ? Do đây chỉ làm việc với một phòng đơn giản nên công việc khá đơn giản là thực hiện việc chiếu hình chiếu vuông góc các điểm của sàn và sàn và vị trí điểm của ghế lên một mặt phẳng duy nhất. Nếu bạn vẫn chưa hiểu rõ cách chiếu thì có thể xem lại bài viết Project Point To A Plane Dynamo Revit API.
| Vector projectPointOnPlane(Vector rVector, Plane plane) | |
| { | |
| Vector vector = rVector - new Vector(plane.origin); | |
| Vector vector1 = vector - plane.normal * Vector.DotProduct(vector,plane.normal); | |
| Vector result = new Vector(plane.origin) + vector1; | |
| return result; | |
| } |
Bây giờ chúng ta hãy tìm ra id của Floor , bạn có thể dễ dàng tìm ra dãy số Id thông qua khung nhìn này. Để xem Id bạn chỉ cần xem bên thanh thông tin bên trái với Id Floor là a9913516192b6e67858af66c5a6862f9
Đối với "Chair", bạn cũng có thể nhanh chóng lấy được id của Chair với id là b7a1a3349fde87a6f699656daef20e7a
Được rồi giờ chúng ta có thể sử dụng API Speckle.Objects, một thư viện mã nguồn mở cho phép chuyển đổi để đọc thông tin đối tượng và lấy về các điểm đường bao của Floor và Chair nhanh chóng. Với việc tùy chỉnh lại một chút kiểm tra điểm để phù hợp với kết quả trả về từ thông tin đối tượng của Speckle.
| bool IsPointInPoly(List<Vector> coordinates, Vector testPoint) | |
| { | |
| bool result = false; | |
| int j = coordinates.Count() - 1; | |
| for (int i = 0; i < coordinates.Count(); i++) | |
| { | |
| if (coordinates[i].y < testPoint.y && coordinates[j].y >= testPoint.y || | |
| coordinates[j].y < testPoint.y && coordinates[i].y >= testPoint.y) | |
| { | |
| if (coordinates[i].x + (testPoint.x - coordinates[i].y) / (coordinates[j].y - coordinates[i].y) * | |
| (coordinates[j].x - coordinates[i].x) < testPoint.x) | |
| { | |
| result = !result; | |
| } | |
| } | |
| j = i; | |
| } | |
| return result; | |
| } |
Ta đa, và bây giờ thì chúng ta sẵn sàn kiểm tra nhanh kết quả trả về từ Speckle xem việc kiểm tra có chính xác không. Với Floor cần lấy là a9913516192b6e67858af66c5a6862f9 và Chair với id là b7a1a3349fde87a6f699656daef20e7a.
Đối với Floor, chúng ta sẽ lấy các điểm bao còn với Chair thì lấy vị trí của nó. Kết quả trả về True tức là nằm trong Floor và False nằm ngoài Floor.
| using Objects; | |
| using Objects.BuiltElements.Revit; | |
| using Objects.Geometry; | |
| using Speckle.Core.Api; | |
| using Speckle.Core.Credentials; | |
| using Speckle.Core.Models; | |
| using Speckle.Core.Transports; | |
| using Point = Objects.Geometry.Point; | |
| using Stream = Speckle.Core.Api.Stream; | |
| Account account = AccountManager.GetDefaultAccount(); | |
| Stream stream = new Stream() {id = "ef2f634638", name = "Test"}; | |
| ServerTransportV2 serverTransportV2 = new ServerTransportV2(account, stream.id); | |
| string chairId = "b7a1a3349fde87a6f699656daef20e7a"; | |
| Base chair = Operations.Receive(chairId,serverTransportV2).Result; | |
| FamilyInstance familyInstance = chair as FamilyInstance; | |
| Point basePoint = familyInstance.basePoint; | |
| Plane plane = new Plane(); | |
| plane.origin = basePoint; | |
| plane.normal = new Vector(0,0,1); | |
| Vector vector = new Vector(basePoint); | |
| string floorId = "a9913516192b6e67858af66c5a6862f9"; | |
| Base floor = Operations.Receive(floorId,serverTransportV2).Result; | |
| RevitFloor? revitFloor = floor as RevitFloor; | |
| Polycurve polycurve = (Polycurve) revitFloor.outline; | |
| List<ICurve> segments = polycurve.segments; | |
| List<Vector> points = new List<Vector>(); | |
| foreach (ICurve segment in segments) | |
| { | |
| if (segment is Line) | |
| { | |
| Line line = (Line) segment; | |
| Vector pointOnPlane = projectPointOnPlane(new Vector(line.start), plane); | |
| points.Add(pointOnPlane); | |
| } | |
| } | |
| Vector famVec = projectPointOnPlane(vector, plane); | |
| bool pointInPoly = IsPointInPoly(points, famVec); | |
| Console.WriteLine(pointInPoly); |
Kết quả : True : Điều đó có nghĩa là chiếc ghế này thuộc về Floor đã kiểm tra.
Như vậy với việc kiểm tra điểm có thuộc room không bây giờ đối với bạn chỉ còn là quá trình kiểm tra chiều cao của phòng nữa mà thôi. Mình để ở đây cho bạn tiếp tục nhé. Đến đây thì xem như mọi vấn đề và mục đích đã giải quyết toàn bộ. Việc kiểm tra Chair có thuộc Floor hay không cũng như kiểm tra điểm nằm trong đường bao và kiểm tra một điểm nằm trong phòng. Hay nói cách khác chính là kiểm tra một chiếc ghế có nằm trong phòng hay không và không phụ thuộc vào các phần mềm AEC nữa. Đó cũng là điều mà bài viết này cuối cùng muốn hướng đến.
Tổng kết
Như vậy rõ ràng với những thuật toán trên, bạn có thể tạo ra hoàn toàn những gì bạn muốn và chỉnh sửa nó. Tùy theo điều kiện ngữ cảnh mà có thể sử dụng áp dụng cho tính toán một family trong phòng hoặc thậm chí bạn có thể xem đây và vấn đề cốt lõi cho việc sử dụng với các bài toán tương tự khác.
Vậy mình cũng đã làm sáng tỏ phần nào sâu xa bên trong những gì mà bạn muốn tìm hiểu, bạn có thể sử dụng các tài liệu tham khảo bên dưới để xem chi tiết thêm.
Cuộc sống
Antikythera mechanism có thể được coi là máy tính đầu tiên trên thế giới. Cỗ máy Antikythera là một máy tính analog và mô hình hệ mặt trời cơ học phát minh bởi người Hy Lạp cổ đại được sử dụng để dự đoán vị trí của các sự kiện thiên văn và nhật thực cho các mục đích về lịch và chiêm tinh trong nhiều thập niên trước. Trông có vẻ chúng ta chưa biết nhiều những thứ bí ẩn mà chúng ta chưa thể khám phá về những gì trước đây mà chúng ta đã tạo ra. Liệu công nghệ trước đây có vượt xa công nghệ mà chúng ta đang nhìn thấy ngày nay ?
